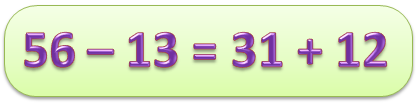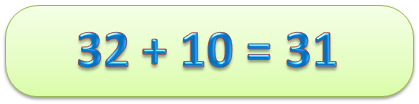Числовые равенства
Чтобы получить запись, называемую числовым равенством, надо два числовых выражения соединить знаком равенства (=).
Пример:
Представленный пример является верным числовым равенством, но числовое равенство может быть неверным:
Давайте разберем свойства числовых равенств.
- Если числовое равенство верно, то прибавив к обеим частям этого равенства одно и тоже число мы получим верное числовое равенство.
Например:
Проверим равенство
(12 + 3) = (9 + 6)
12 + 3 = 15 и 9 + 6 = 15
Равенство верно, теперь проверим свойство
(12 + 3) + (5 – 2) = (9 + 6) + (5 – 2)
15 + (5 – 2) = 15 + (5 – 2)
18 = 18
В обоих случаях равенства верны
То же самое произойдет, если мы вычтем одно и то же числовое выражение из обеих частей верного числового равенства.
Проверим это свойство на предыдущем примере заменив действие сложение на вычитание:
(12 + 3) – (5 – 2) = (9 + 6) – (5 – 2)
15 + (5 – 2) = 15 + (5 – 2)
12 = 12
Как мы видим равенство верно.
- Если числовое равенство верно, то умножив обе части этого равенства на одно и тоже числовое выражение мы получим верное числовое равенство.
Проверим и это свойство:
(75 – 3) = (15 + 57)
75 – 3 = 72 и 15 + 57 = 72 это равенство верно
(75 – 3) · (10 – 2) = (15 + 57) · (10 – 2)
72 · (10 – 2) = 72 · 8 = 576
576 = 576
Свойство доказано.
- Если числовое равенство верно, то разделив обе части этого равенства на одно и тоже числовое выражение мы получим верное числовое равенство. Правда, это выражение справедливо только если числовое выражение не равно нулю, так как на ноль делить нельзя.
Проверим это свойство:
(12 + 3) : (5 – 2) = (9 + 6) : (5 – 2)
15 : 3 = 15 : 3
5 = 5
Что и требовалось доказать.
Числовые неравенства
Если одно числовое выражение не равно другому, то сравним оба выражения поставим между ними знак сравнения – больше (>) или меньше (<). Мы получим числовое неравенство.
(3 · 4) < (3 · 6)
(10 + 25)
Числовые неравенства также могут быть верными и неверными:
(25 – 5) : 5 > 10 – это неравенство неверно
(25 – 5) : 5 < 10 – это неравенство верно
Спасибо, что Вы с нами!