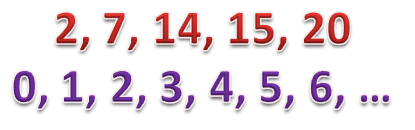Мы каждый день отвечаем на вопрос «сколько?». При этом помимо слов много или мало, мы называем конкретные числа.
Число является основным понятием математики, которое сложилось в ходе очень длительного исторического развития.
А чтобы ответить на вопрос «сколько?» надо сосчитать.
Числа, которые мы получаем в результате счета называются натуральными числами.
Название «натуральное» происходит от латинского слова natura – природа. То есть натуральные числа как бы происходят от природы, но, конечно, изобретены человеческим мозгом.
А впервые термин «натуральное число» появляется в трудах римского философа Боэция, жившего в V – VI веке.
Самое маленькое натуральное число 1. А вот самого большого натурального числа не существует.
Для того, чтобы получить следующее натуральное число надо прибавить к текущему натуральному числу 1.
Нет наибольшего натурального числа.
Натуральных чисел бесконечно много, а вот несуществующих предметов человеку не приходило в голову считать. Поэтому 0 не натуральное число, так как оно не может получиться в результате счета.
Число 0 не является натуральным числом.
Считается, что 0 получился в результате изобретения вычитания и с потребностью обозначить то, что в результате некоторых вычислений не остается ни одного предмета.
Но давайте поговорим об известном человеку наибольшем натуральном числе.
Число, которое считается самым большим натуральным числом, называется «гугол». Чтобы представить это число не хватит воображения, а чтобы сосчитать от 1 до гугола нам не хватит жизни. Записать число гугол сложно, так как нам понадобится изобразить после единицы сто нулей:
Располагая все натуральные числа в порядке возрастания, мы получаем натуральный ряд чисел.
Натуральный ряд записывается, начиная с 1 и далее в порядке возрастания, не пропуская ни одного числа, в конце ряда ставится многоточие:
Многоточие указывает на бесконечность натурального ряда.
Итак, ряды, изображенные на следующем рисунке, не являются натуральными:
В первом случае ряд начинается не с 1, а также в нем пропущены некоторые числа. Во втором случае ряд начинается с нуля, а это число, как мы говорили ранее, не является натуральным. Такой ряд иногда называют расширенным натуральным рядом.
Известно два натуральных ряда, это ряд количественных и порядковых чисел.
Когда мы считаем (один, два, три и так далее), мы получаем ряд количественных чисел. Количественные числа отвечают на вопрос «сколько?», они называются количественными числительными.
А вот порядковые числительные указывают на место, которое занимает какой-либо предмет: пятый день, шестая строка, четвертый квадрат и так далее.
Арифметические действия выполняются только над количественными числами, поэтому их иногда называют арифметическими.
А вот такие ряды как:
называются отрезком натурального ряда чисел. Даже одно число, например 10, можно назвать отрезком натурального ряда чисел.
Если числа в отрезке ряда перечислены не по порядку или хотя бы одно число пропущено или числа перечислены в обратном порядке, то такой отрезок ряда не является натуральным.
Если надо записать очень длинный отрезок ряда чисел можно записать часть отрезка ряда, затем поставить многоточие, а затем записать несколько последних чисел ряда. Это может выглядеть так:
Спасибо, что Вы с нами!