Ранее мы говорили о порядке выполнения математических действий. Продолжим изучение математических законов и сегодня поговорим о следующем:
- о переместительном законе сложения;
- о сочетательном законе сложения;
- о переместительном законе умножения;
- о сочетательном законе умножения;
- о распределительном законе.
Переместительный закон сложения
У Маши 3 яблока, а у Миши 4. Сколько яблок у детей?
Для решения этой задачи надо сложить вместе 3 Машиных яблока и 4 Мишиных:
3 + 4 = 7
Ответ: У детей 7 яблок.
А изменится ли ответ если яблоки складывать в другом порядке, то есть к 4 Мишиным прибавить 3 Машиных яблока?
4 + 3 = 7
Мы убедились, что не важно, в каком порядке складывать числа (слагаемые). Результат (сумма) будет одинаковым:
3 + 4 = 4 + 3 = 7
Это и есть переместительный закон сложения, он звучит так:
От перемены мест слагаемых сумма не меняется.
Сочетательный закон сложения
В двух коробках лежат фломастеры по 80 штук в каждой. В одну коробку положили ещё 23 фломастера. Сколько всего стало фломастеров?
Эту задачу можно решить следующим образом:
(80 + 23) + 80 = 183
или так:
80 + (80 + 23) = 183
Результат получается один и тот же:
(80 + 23) + 80 = 80 + (80 + 23) = 183
Отсюда следует важное правило вычислений:
Складывая несколько слагаемых, можно группировать их в любом порядке.
Переместительный закон умножения
Катя купила 5 булочек по 20 рублей, а Коля 20 булочек по 5 рублей. Кто заплатил больше денег?
Итак, вычислим, сколько заплатила Катя:
5 × 20 = 100
Теперь вычислим, сколько заплатил Коля:
20 × 5 = 100
Мы видим, что результат одинаковый. Катя и Коля заплатили одинаковые суммы.
В результате решения этой задачи мы убедились, что не важно, в каком порядке перемножать числа (множители), результат (произведение) получится один и тот же:
5 × 20 = 20 × 5 = 100
Это и есть переместительный закон умножения, он звучит так:
От перемены мест множителей произведение не меняется.
Сочетательный закон умножения
В упаковке 6 пакетов сока. В контейнер входит 10 таких упаковок. Сколько пакетов сока входит в 5 таких контейнеров.
Решим эту задачу, вычислим, сколько пакетов сока в контейнере, а затем в 5 контейнерах:
(6 × 10) × 5 = 300
Можно вычислить сначала, сколько упаковок в 5 контейнерах, а затем, сколько всего пакетов сока:
6 × (10 × 5) = 300
Как бы мы не считали, получаем одинаковый результат:
(6 × 10) × 5 = 6 × (10 × 5) = 300
Таким образом, мы убедились в справедливости сочетательного закона умножения:
Перемножая множители, можно их группировать в любом порядке.
Распределительный закон
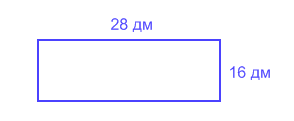
Вспомним, как можно вычислить периметр прямоугольника, длина которого 28 дм, а ширина 16 дм. Попробуем это сделать разными способами.
Итак, мы знаем, что для вычисления периметра прямоугольника, надо сложить длины всех его сторон:
28 + 28 + 16 + 16 = 88
Учитывая то, что в прямоугольнике 2 длины и 2 ширины можно вычислить периметр следующим способом:
28 × 2 + 16 × 2 = 88
Но ведь можно сложить длину и ширину и умножить на 2:
( 28 + 16) × 2
Таким образом, мы убедились, что можно сначала сложить длину и ширину, а затем умножить на 2, или сначала удвоить длину и ширину, а затем их сложить:
( 28 + 16) × 2 = 28 × 2 + 16 × 2 = 88
Решая нашу задачу, мы доказали справедливость распределительного закона:
Чтобы умножить сумму на число, можно умножить каждое слагаемое на это число и потом сложить полученные произведения.
Решим ещё один пример:
(7 + 3) × 4
Значение данного выражения можно найти разными способами:
Выполнив действия по порядку:
(7 + 3) × 4 = 10 × 4 = 40
Или применив правило умножения суммы на число:
(7 + 3) × 4 = 7 × 4 + 3 × 4 = 28 + 12 = 40
В результате разных способов вычисления, мы получили одинаковый результат.
Спасибо, что Вы с нами.