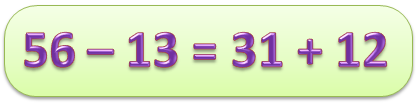В этой статье начинается рубрика «основные содержательные линии в курсе математики начальной школы». Здесь мы разберем, как развивается изучение основных математических понятий с каждым классом начальной школы. Мы рассмотрим такие основные линии, как:
- изучение нумерации;
- изучение величин;
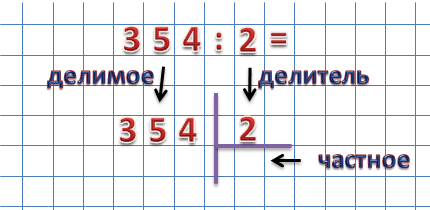
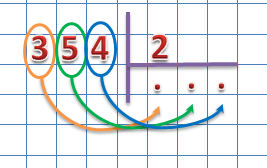
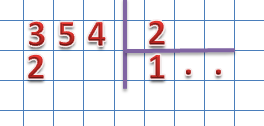
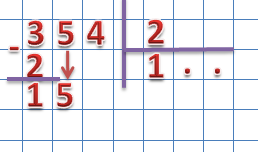
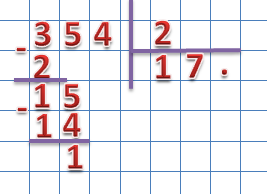
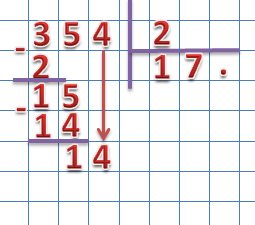
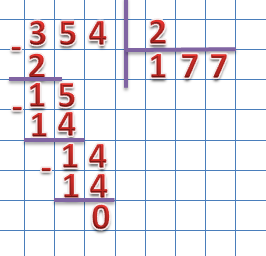
- освоение вычислительных навыков;
- значение выражений;
- решение текстовых задач;
- решение уравнений;
- геометрический материал.
Итак, начнем по порядку.
Изучение нумерации
В первом классе наши дети изучают числа до 100. Чтение, запись и последовательность, а также десятичный состав. Далее во втором классе изучаются уже сотни до тысячи.
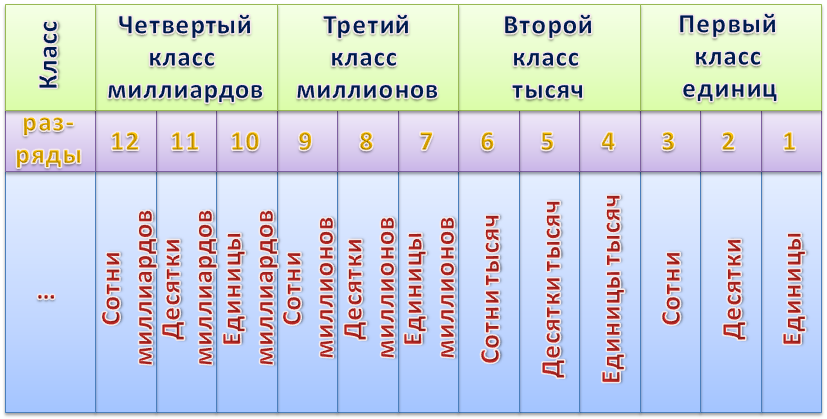
Изучается разрядность – единицы, десятки и сотни. Затем в третьем классе изучаются числа до 10000 – чтение, запись, последовательность и разрядный состав.
И наконец, в четвертом классе изучаются числа до 1000000.
Изучение величин
Единицы длины начинают изучаться в первом классе с такой величины, как сантиметр. Во втором классе изучаются такие величины, как миллиметр, метр и километр. Изучаются соотношения: 1см = 10мм, 1м = 100см, 1км = 1000м. Дети учатся переводить сантиметры в миллиметры. В третьем классе изучается величина дециметр и соотношения: 1дм = 10см, 1м = 10дм. Переводятся метры в сантиметры, сантиметры в дециметры и обратно. И, наконец, в четвертом классе, дети, продолжая переводить разные величины учатся переводить километры в метры, метры в дециметры, дециметры в миллиметры и обратно.
Единицы площади начинают изучаться со второго класса такими величинами, как квадратный метр, квадратный сантиметр и квадратный километр. В третьем классе используются названия единиц площади в задачах. В четвертом классе дети узнают такие величины, как квадратный дециметр, ар, гектар, квадратный километр. Изучаются соотношения: 1 кв.см = 100 кв.мм, 1 кв.дм = 100 кв.см, 1 кв.м = 100 кв.дм.
Единицы вместимости – в первом классе встречается название литр. Во втором – используются единицы вместимости в задачах, как и в третьем и в четвертом классе.
Единицы времени начинают изучать во втором классе с таких величин, как час и минута. Дети узнают соотношение 1ч = 60 мин. В третьем классе уже изучаются секунды, сутки, неделя, месяц, год и их соотношения: 1мин = 60с, 1сут = 24ч, 1неделя = 7 суткам, 1 год = 365 (366) суткам. А также перевод часов в минуты, минут с секунды, сутки в часы и обратно. В четвертом классе проходят такие величины, как век, тысячелетие и соотношение: 1век = 100годам.
Единицы скорости начинают изучаться с третьего класса с названий: км/ч, км/мин, км/с, м/мин и м/с. В четвертом классе используются названия единиц скорости в задачах.
Единицы массы изучаются с первого класса и начинаются с названия – килограмм. Во втором классе используются названия единиц массы в задачах. В третьем классе уже изучаются величины: тонна, грамм, килограмм и их соотношения: 1кг = 1000г, 1т = 1000кг, а также перевод единиц: килограммы в граммы и обратно. В четвертом классе изучается название центнер и соотношения: 1ц = 100кг, 1т = 10ц, а также перевод килограммов в центнеры, килограммов в тонны, центнеры в тонны и обратно.
В следующих статье этого цикла мы рассмотрим тему “вычислительные навыки” .
