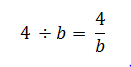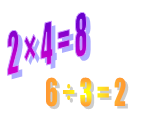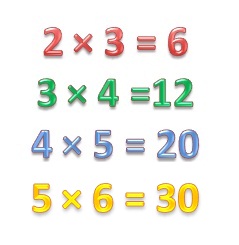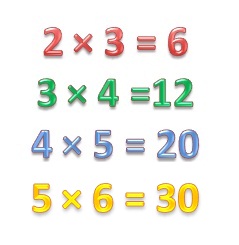Выражения с переменными. Буквенные равенства и неравенства.

19 Март 2023 Рубрика: Математика, элементы алгебры
Ваш отзыв

Выражения с переменными

Выражениями с переменными называются выражения содержащие переменные.

В качестве переменных в выражениях используются буквы, поэтому их также называют буквенными выражениями. Буквенные выражения могут содержать как несколько букв, так и одну букву.

Например:

Выражения с перменными

 

буквенные выражения

 

В задачах и примерах буквенные выражения используются для вычисления выражений с заданными переменными. То есть вместо букв надо подставить заданные значения:

Вычислить выражение

VsP31

Подставляем в выражение значения вместо букв:

VsP32

Произведения с переменными записывают без знака умножения (·):

VsP33

Если в выражениях участвует деление, такие выражения записывают в виде дроби:

VsP3

Соответственно выражение в предыдущем примере можно записать следующим образом:

VsP4

Давайте рассмотрим ещё один пример:VsP5

при x = 2

Если в выражении встречается несколько раз одна и та же буква (переменная), то ей соответствует одно и то же значение.

В таком случае решение будет следующим:

VsP6 Читать полностью »

, , , , ,
Подробно

Деление и другие математические действия

26 Сен 2020 Рубрика: Математика
Ваш отзыв

Мы уже говорили о делении и об основных правилах деления. Продолжим изучать деление и разберем, как можно упростить некоторые примеры с участием деления, такие как:

  1. Деление произведения двух чисел на число;
  2. Деление числа на произведение двух чисел;
  3. Деление суммы двух чисел на третье число;
  4. Деление разности двух чисел на третье число;
  5. Сумма или разность двух частных, в которых делители одинаковы.

Деление произведения двух чисел на число

Чтобы разделить произведение двух чисел на число, разделите на это число один из множителей, а полученное частное умножьте на второй множитель.

del_id1

Например:

36 × 7 ÷ 4 = (36 ÷ 4) × 7 = 9 × 7 = 63

15 × 44 ÷ 11 = (44 ÷ 11) × 15 = 4 × 15 = 60

Если ни один из множителей не делится на третье число, то следует вычислить произведение двух первых чисел и потом поделить на третье число.

15 × 24 ÷ 9 = 360 ÷ 9 = 40

Деление числа на произведение двух чисел

Чтобы разделить число на произведение двух чисел, разделите это число на один из множителей, а затем полученное частное разделите на другой множитель.

2. Деление числа на произведение двух чисел

Например:

432 ÷ (36 × 6) = 432 ÷ 36 ÷ 6 = 2

3072 ÷ (12 × 32) = 3072 ÷ 12 ÷ 32 = 8

Этот прием называется приемом последовательного деления.

Деление суммы двух чисел на третье число

Чтобы разделить сумму двух чисел на третье число, разделите каждое слагаемое суммы на это число, а затем сложите полученные частные.

3. Деление суммы двух чисел на третье число

Например:

(28 + 42) ÷ 7 = 28 ÷ 7 + 42 ÷ 7 = 10

Если числа в скобках не делятся на третье число, то вычисляем по правилам «порядка выполнения математических действий».

(115 + 95) ÷ 6 = 35

Для удобства деления представьте делимое суммой двух чисел:

96 ÷ 8 = (40 + 56) ÷ 8 = 40 ÷ 8 + 56 ÷ 8 = 12 Читать полностью »

, ,
Подробно

Загадочные простые числа

19 Июль 2019 Рубрика: Занимательная математика, Математика
Отзывов (3) »

Еще со времен древних греков простые числа были очень привлекательны для математиков. Они постоянно ищут разные способы их нахождения, но самым эффективным способом «поимки» простых чисел, считается способ, найденный александрийским астрономом и математиком Эратосфеном. Этому способу уже около 2000 лет.

какие числа простые

Какие числа являются простыми

Как же определить простое число? Многие числа делятся без остатка на другие числа. Число, на которое делится целое число, мы называем делителем.

В данном случае мы говорим о делении без остатка. Например, число 36 можно разделить на 1, 2, 3, 4, 6, 9, 12, 18 и на само себя, то есть на 36. Значит, 36 имеет 9 делителей. Число 23 делится только на себя и на 1, то есть это число имеет 2 делителя – это число является простым.

Числа, которые имеют только два делителя, называются простыми числами. То есть, число, которое делится без остатка только на себя и на единицу, называется простым.

Для математиков открытие закономерностей в ряду чисел, которые потом можно использовать для построения гипотез, является очень приятным событием. Но простые числа отказываются подчиняться хоть какой-нибудь закономерности. Но есть способ определения простых чисел. Этот способ найден Эратосфеном, он называется «решетом Эратосфена». Давайте рассмотрим вариант такого «решета», представленный в виде таблицы чисел до 48 и поймем, как она составлена.

решето эратосфена

В этой таблице все простые числа меньше 48 отмечены оранжевым цветом. Найдены они так:

  • 1 – имеет единственный делитель и поэтому не является простым числом;
  • 2 – наименьшее простое число и единственное четное, так как все остальные четные числа делятся на 2, то есть имеют не меньше 3 делителей, эти числа сведены в фиолетовую колонку;
  • 3 – простое число, имеет два делителя, все остальные числа, которые делятся на 3, исключаются – эти числа сведены в желтую колонку. Колонка, отмеченная и фиолетовым, и желтым, содержит числа делящиеся и на 2 и на 3;
  • 5 – простое число, все числа, которые делятся на 5, исключаются – эти числа обведены зеленым овалом;
  • 7 – простое число, все числа, которые делятся на 7, обведены красным овалом – они не являются простыми;

Все числа не являющиеся простыми отмечены синим цветом. Далее эту таблицу можно составить самому по образу и подобию.

Самое большое число, которое рассчитано математиками, записывается 25962 знаками.

Если вы хотите получать анонсы наших статей, подпишитесь на рассылку “Новости сайта”.

, ,
Подробно

Основные содержательные линии в математике – вычислительные навыки

13 Янв 2017 Рубрика: Математика
Отзывов (3) »

вычислительные навыки в начальной школеПродолжаем тему  «основные содержательные линии курса математики начальной школы». В предыдущей статье мы рассмотрели такие линии, как «нумерации» и «величины». Продолжим далее по списку, представленному в предыдущей статье, и рассмотрим освоение учениками начальной школы вычислительных навыков.

Сложение и вычитание

В первом классе начальной школы дети осваивают сложение и вычитание в пределах 10, а также в пределах 100 без перехода через десяток.

Во втором классе сложение и вычитание осваивается уже сначала в пределах 20 с переходом через десяток, затем в пределах 100, также с переходом через десяток. Также осваивается письменное вычисление двухзначных чисел «в столбик».

В третьем классе осваивается сложение с переходом через разряд в пределах 10000, а также вычитание с переходом через разряд в пределах 1000. Дети устно складывают и вычитают круглые числа в пределах 1000, письменно – трехзначные числа.

В четвертом классе осваивается сложение и вычитание многозначных чисел, уже в пределах 1000000. Устно складывают и вычитают круглые числа, такие как тысячи и миллионы, а письменно – многозначные числа в пределах миллиона.

На нашем сайте Вы можете посмотреть видеоуроки сложение и вычитание.

Умножение и деление

Освоение таких вычислительных навыков, как умножение и деление начинается со второго  класса, здесь осваивается таблица умножения, а также соответствующие случаи деления.

В третьем классе осваивается умножение трехзначных чисел на однозначное число, а также деление с остатком. Деление осуществляется трехзначных чисел на однозначное число, берутся простые случаи. Устно осуществляется внетабличное умножение двухзначных чисел на однозначные, умножение и деление на 10 и на 100, а также умножение и деление десятков на однозначное число. Письменно умножаются и делятся трехзначные числа на однозначные.

В четвертом классе осваивается умножение и деление многозначных чисел на двухзначные и трехзначные числа в пределах миллиона. Устно вычисляются круглые числа, а именно умножение и деление на двузначное число в пределах 100. Письменно умножаются и делятся многозначные числа на двузначные и трехзначные числа.

О том, что такое умножение и деление Вы можете прочитать на нашем сайте, а также здесь Вы можете найти информацию о том как выучить таблицу умножения.

На этом мы прервем наши исследования и продолжим их в следующей статье “найти значение выражения“.

Если вы хотите получать информацию о новых статьях и проектах нашего сайта, то подпишитесь на рассылку новостей сайта. Всего вам наилучшего и успехов. Спасибо.

, , , , ,
Подробно

Деление в столбик

20 Сен 2016 Рубрика: Математика
Отзывов (2) »

Деление многозначных или многоразрядных чисел удобно производить письменно в столбик. Давайте разберем, как это делать. Начнем с деления многоразрядного числа на одноразрядное, и постепенно увеличим разрядность делимого.

Итак, поделим 354 на 2. Для начала разместим эти числа как показано на рисунке:

деление в столбик

Делимое размещаем слева, делитель справа, а частное будем записывать под делителем.

Теперь начинаем делить делимое на делитель поразрядно слева на право. Находим первое неполное делимое, для этого берем первый слева разряд, в нашем случае 3 и сравниваем с  делителем.

3 больше 2, значит 3 и есть неполное делимое. Ставим точку в частном и определяем, сколько ещё разрядов будет в частном – столько же, сколько осталось в делимом после выделения неполного делимого. В нашем случае в частном столько же разрядов, сколько в делимом, то есть старшим разрядом будут сотни:

delen_v_st_2

Для того чтобы 3 разделить на 2 вспоминаем таблицу умножения на 2 и находим число при умножении которого на 2 получим наибольшее произведение, которое меньше 3.

2 × 1 = 2               (2 < 3)

2 × 2 = 4               (4 > 3)

2 меньше 3, а 4 больше, значит, берем первый пример и множитель 1.

Записываем 1 в частное на место первой точки (в разряд сотен), а найденное произведение записываем под делимым:

delen_v_st_3

Теперь находим разность, между первым неполным делимым и произведением найденного разряда частного и делителем:

delen_v_st_4

Далее находим второе неполное делимое, для этого значение следующего разряда делимого опускаем к разности:

delen_v_st_5

Полученное значение сравниваем с делителем. 15 больше 2, значит, мы нашли второе неполное делимое. Для того чтобы найти результат деления 15 на 2 вновь вспоминаем таблицу умножения на 2 и находим наибольшее произведение, которое меньше 15:

2 × 7 = 14             (14 < 15)

2 × 8 = 16             (16 > 15)

Искомый множитель 7, записываем его в частное на место второй точки (в десятки). Находим разность между вторым неполным делимым и произведением найденного разряда частного и делителя:

delen_v_st_6

Продолжаем деление, для чего находим третье неполное делимое. Спускаем следующий разряд делимого:

delen_v_st_7

Делим неполное делимое на 2, полученное значение ставим в разряд единиц частного. Проверим правильность деления:

2 × 7 = 14

Результат деления третьего неполного делимого на делитель пишем в частное, находим разность:

delen_v_st_8

Разность мы получили равную нулю, значит деление произведено правильно.

Читать полностью »

,
Подробно

Числовые равенства и неравенства

16 Янв 2015 Рубрика: Математика
Ваш отзыв

Числовые равенства

Чтобы получить запись, называемую числовым равенством, надо два числовых выражения соединить знаком равенства (=).

Пример:

Числовые равенства

Представленный пример является верным числовым равенством, но числовое равенство может быть неверным:

Неверное числовое равенство

Давайте разберем свойства числовых равенств.

  1. Если числовое равенство верно, то прибавив к обеим частям этого равенства одно и тоже число мы получим верное числовое равенство.

первое свойство числовых равенств

Например:

Проверим равенство

(12 + 3) = (9 + 6)

12 + 3 = 15 и 9 + 6 = 15

Равенство верно, теперь проверим свойство

(12 + 3) + (5 – 2) = (9 + 6) + (5 – 2)

15 + (5 – 2) = 15 + (5 – 2)

18 = 18

В обоих случаях равенства верны

 

То же самое произойдет, если мы вычтем одно и то же числовое выражение из обеих частей верного числового равенства.

второе свойство числовых равенств

Проверим это свойство на предыдущем примере заменив действие сложение на вычитание:

(12 + 3) – (5 – 2) = (9 + 6) – (5 – 2)

15 + (5 – 2) = 15 + (5 – 2)

12 = 12

Как мы видим равенство верно.

 

  1. Если числовое равенство верно, то умножив обе части этого равенства на одно и тоже числовое выражение мы получим верное числовое равенство.

третье свойство числовых равенство

Проверим и это свойство:

(75 – 3) = (15 + 57)

75 – 3 = 72 и 15 + 57 = 72 это равенство верно

(75 – 3) · (10 – 2) = (15 + 57) · (10 – 2)

72 · (10 – 2) = 72 · 8 = 576

576 = 576

Свойство доказано.

Читать полностью »

, , ,
Подробно

Деление. Основные правила

30 Июль 2012 Рубрика: Математика
Ваш отзыв

деление чиселОдним из простых арифметических действий является деление. Мы знаем, что умножение мы можем представить, как сложение числа самого с собой столько раз, на сколько нам надо его умножить.

Деление можно представить, как многократное вычитание. Давайте рассмотрим этот вопрос поподробнее.

Деление чисел

Рассмотрим картинку.

На картинке мы видим 12 яблок на блюде. Яблоки разделены на четыре группы по 3 яблока. Записать это можно так:

12 ÷ 4 = 3

Число, которое мы делим, называется делимым, число на которое мы делим, называется делителем, а результат деления называется частным. В нашем примере делимое 12, делитель 4, а частное 3.

Деление можно проверить умножением:

3 × 4 = 12

А также деление можно проверить, многократным вычитанием:

12 – 3 – 3 – 3 – 3 = 0

Мы видим, что если из 12 вычесть 4 раза 3, то получится ноль. Значит, 12 на 4 делится без остатка.

Рассмотрим другой пример, разделим 13 на 4.

деление с остатком

Из рисунка видно, что при делении 13 яблок на 4 получился 3 и остаток – одно яблоко.

13 ÷ 4 = 3 (ост.1)

Проверим вычитанием:

13 – 3 – 3 – 3 – 3 = 1

Мы видим, что если из 13 четыре раза вычесть число 3, то останется 1. Наш пример называется делением с остатком. Здесь 13 – делимое, 4 – делитель, а 3 – неполное частное, 1 – остаток от деления.

Теперь проверим умножением:

3 × 4 + 1 = 13

  Читать полностью »

, ,
Подробно

Таблица умножения

03 Июль 2012 Рубрика: Математика, Основные правила
Отзывов (3) »

учить таблицу умноженияМы все знаем, что учить таблицу умножения необходимо. А необходимо потому, что зная назубок таблицу умножения/деления от 1 до 10, ребенок без труда освоит внетабличное умножение и деление. Но как же легче всего выучить таблицу умножения. Ответ неоднозначен, для каждого ребенка нужен индивидуальный подход. Но все же можно дать общие для всех советы.
Для начала надо объяснить ребенку, что такое умножение. Умножение связано с действием сложения. Объясните ребенку, что перемножаемые числа называются множителями, а полученное число называется произведением.

Итак, начинаем с умножения на 2:
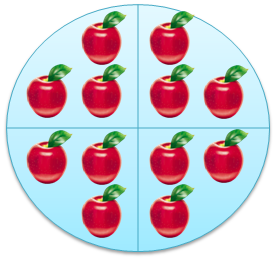
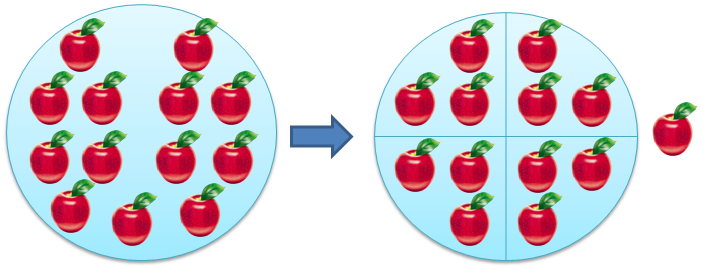
Что такое 2 × 2, это 2 + 2 и равно 4. Положим две конфеты на одну тарелочку и еще две конфеты на другую. Если конфеты сосчитать все вместе получится четыре, то есть 2 конфеты умножить на 2 тарелочки, получится 4 конфеты: 2 × 2 = 4.

Теперь, чтобы проверить результат, разделите 4 конфеты обратно на две тарелки: 4 ÷ 2 = 2.

математика таблица умножения
А как еще можно поровну разделить конфеты? Конечно же, по четырем тарелкам. Если на каждую тарелку положить по конфете:

4 ÷ 4 = 1

4 ÷ 1 = 4

 проверим: 4 × 1 = 4.

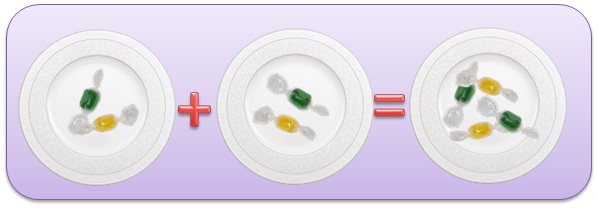
Теперь добавим на каждую тарелочку еще по конфете. Считаем все конфеты, получаем 6, как получилось? Три конфеты умножили на две тарелочки: 3 × 2 = 3 + 3 = 2 + 2 + 2 = 6.

То есть три умножить на два это 2 раза по 3 или 3 раза по 2, и если взять три тарелочки по две конфеты, то все равно получится 6 конфет.

урок таблица умножения

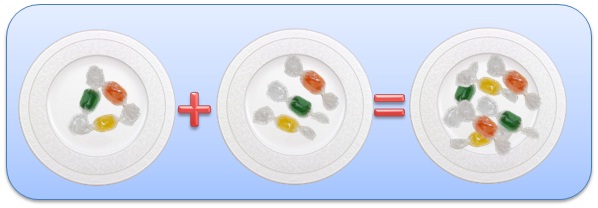
От перемены мест множителей произведение не меняется: 3 × 2 = 2 × 3 = 6.

Теперь деление: 6 ÷ 2 = 3, берем 6 конфет и раскладываем поровну на две тарелки, получаем на каждой по три конфеты. Также показываем деление шести конфет по трем тарелкам, получаем по две конфеты на каждой тарелке: 6 ÷ 3 = 2.

Таким образом, можно разобрать каждый пример умножения на 2, на 3 и так далее.
Когда ребенок уверенно будет решать такого рода примеры, приступайте к постепенному заучиванию таблицы умножения, сначала на 2, потом на 3 и так далее до 9.

Объясните особенности умножения на 1 и на 10:

При умножении любого числа на 1, в результате получите это же число:

1 × 1 = 1

 1 × 2 = 2

 1 × 3 = 3

 1 × 99 = 99

и так далее.

При умножении любого числа на 10, в результате получим то же число, но с добавленным справа нулем: 10 × 3 = 30, один ноль, потому что в цифре 10 один ноль, а если умножать не на 10, а на 100, то получим справа два нуля: 100 × 3 = 300. И так далее с 1000, 10000…

То есть для того, чтобы умножить число на 10, 100, 1000 и так далее (например 4 × 10), сначала вспоминаем правило умножения на 1, то есть пишем то же число (4) и дописываем к нему справа столько нулей, сколько во втором множителе (10), (4 × 10 = 40).

Читать полностью »

, , ,
Подробно