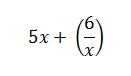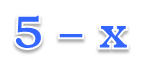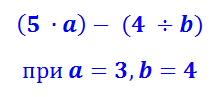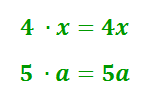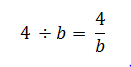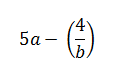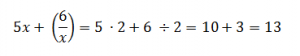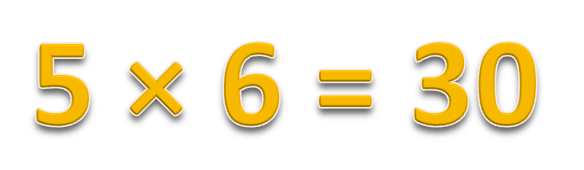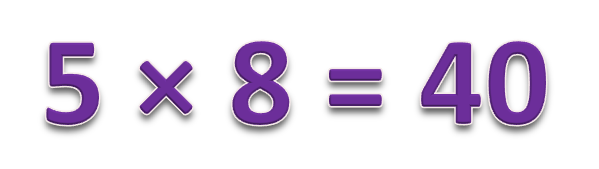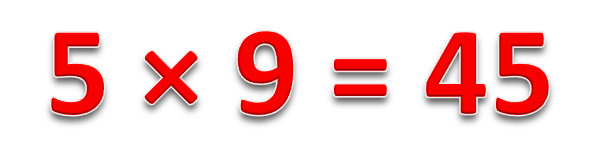интернет проект BeginnerSchool.ru

Как выучить таблицу умножения

13 Март 2023 Рубрика: Математика, Основные правила

Отзывов (10) »

Начиная со второго класса без знания таблицы умножения на зубок учиться сложно. Но выучить таблицу умножения для некоторых детей большая проблема. К моему удивлению я обнаружила, что многие взрослые не знают таблицу умножения. Вся проблема в том, что в свое время не был найден правильный алгоритм запоминания таблицы.

Алгоритмов много, но надо выбрать тот, который подойдет именно вашему ребенку.

Люди не одинаково воспринимают информацию. У кого-то лучше развита зрительная память, а другие лучше запоминают на слух. Поэтому при запоминании таблицы умножения лучше применять оба способа.

Метод, который мы сегодня предложим, не является панацеей, но он проверен и работает.

Обучение следует разбить по дням. Пока не запомнится предыдущее занятие, начинать следующее не стоит. Все дети запоминают с разной скоростью. Возможно, ваш ребенок будет быстро усваивать информацию, а может быть ему понадобиться несколько дней для запоминания одного урока. Это совершенно нормально и не стоит ругать ребенка. Лучше если вы будете терпеливы. Во время занятий должна быть тишина. Выключите музыку, телевизор. Уберите игрушки. Ничего не должно отвлекать ребенка.

Каждая статья сопровождается видеоуроком и тестом. Первый день не очень сложен, поэтому видеоуроков не требует. Если вы пожелаете, мы сделаем видеоурок для первого дня. Пожелания пишите в комментариях под статьей.

В лучшем случае нам понадобится 6 дней на заучивание всей таблицы умножения. Если запоминание идет медленно, можно повторять урок несколько дней до полного усвоения. Здесь вы можете найти ссылки на все уроки:

день первый

день второй

день третий

день четвертый

день пятый

день шестой

После заучивания таблицы умножения мы предлагаем пройти тест:

Читать полностью »

Деление и другие математические действия

26 Сен 2020 Рубрика: Математика

деление, математика, умножение

Мы уже говорили о делении и об основных правилах деления. Продолжим изучать деление и разберем, как можно упростить некоторые примеры с участием деления, такие как:

Деление произведения двух чисел на число;
Деление числа на произведение двух чисел;
Деление суммы двух чисел на третье число;
Деление разности двух чисел на третье число;
Сумма или разность двух частных, в которых делители одинаковы.

Деление произведения двух чисел на число

Чтобы разделить произведение двух чисел на число, разделите на это число один из множителей, а полученное частное умножьте на второй множитель.

Например:

36 × 7 ÷ 4 = (36 ÷ 4) × 7 = 9 × 7 = 63

15 × 44 ÷ 11 = (44 ÷ 11) × 15 = 4 × 15 = 60

Если ни один из множителей не делится на третье число, то следует вычислить произведение двух первых чисел и потом поделить на третье число.

15 × 24 ÷ 9 = 360 ÷ 9 = 40

Деление числа на произведение двух чисел

Чтобы разделить число на произведение двух чисел, разделите это число на один из множителей, а затем полученное частное разделите на другой множитель.

Например:

432 ÷ (36 × 6) = 432 ÷ 36 ÷ 6 = 2

3072 ÷ (12 × 32) = 3072 ÷ 12 ÷ 32 = 8

Этот прием называется приемом последовательного деления.

Деление суммы двух чисел на третье число

Чтобы разделить сумму двух чисел на третье число, разделите каждое слагаемое суммы на это число, а затем сложите полученные частные.

Например:

(28 + 42) ÷ 7 = 28 ÷ 7 + 42 ÷ 7 = 10

Если числа в скобках не делятся на третье число, то вычисляем по правилам «порядка выполнения математических действий».

(115 + 95) ÷ 6 = 35

Для удобства деления представьте делимое суммой двух чисел:

96 ÷ 8 = (40 + 56) ÷ 8 = 40 ÷ 8 + 56 ÷ 8 = 12 Читать полностью »

игры, математика, умножение

Чудеса умножения

16 Апр 2020 Рубрика: Занимательная математика

Отзывов (11) »

С этой статьи мы открываем рубрику «занимательная математика». Математика – это очень интересная наука. При её изучении мы понимаем, что многие процессы можно описать различными математическими выражениями. А главное в ней много занимательных головоломок и шарад. Мы будем рассказывать о таких интересных случаях.

Давайте посмотрим на таблицу умножения на 9:

1 × 9 = 09

2 × 9 = 18

3 × 9 = 27

4 × 9 = 36

5 × 9 = 45

6 × 9 = 54

7 × 9 = 63

8 × 9 = 72

9 × 9 = 81

10 × 9 = 90

Что интересного в этой таблице? Можно отметить, что если 9 умножать на четное число, то получается четное, а если на нечетное, то и получится нечетное число.

Посмотрите внимательно на десятки в результате произведений и на единицы. Просматривая произведения сверху вниз, мы видим десятки как возрастающий ряд: 0,1,2,3,4,5,6,7,8,9, а единицы, как убывающий: 9,8,7,6,5,4,3,2,1,0. А если смотреть снизу вверх, то все наоборот – теперь десятки убывают, а единицы возрастают. Читать полностью »

Учим таблицу умножения. День второй

20 Окт 2019 Рубрика: Математика, Основные правила

1 отзыв »

В предыдущем уроке мы узнали об умножении на 0, на 1 и на 10. Если Вы не читали введения, прочитайте пожалуйста в статье “Как выучить таблицу умножения“, там даны все указания по изучению уроков.

Повторите пройденный материал, сделайте перерыв 15 минут.

Теперь начнем с таблицы умножения на 2. Показываем ребенку пример и проговариваем его 3 раза. Ребенок должен повторять каждый раз за вами и смотреть на пример. Как вы будете чередовать примеры – неважно. Главное разбить примеры на группы:

I группа

Дважды два – четыре

Проговариваем три раза, пример должен быть перед глазами у ребенка, ребенок повторяет за вами.

Дважды три – шесть

Дважды четыре – восемь

Заучив все три примера, спросите у ребенка, сколько будет дважды три. Ребенок точно должен ответить. Сразу за ответом следующий вопрос: сколько будет дважды два, после правильного ответа – вопрос: сколько будет дважды четыре. Специально, при проверке чередуем примеры не по порядку. Если ребенок ошибся, повторите пример с ответом, показывая пример, опять три раза.

Когда ребенок правильно ответил на все вопросы, делаем перерыв минут десять. Во время перерыва ребенок должен заниматься чем угодно, но не видеть и не повторять примеры. Отвлекаясь, его мозг будет усваивать информацию.

После перерыва опять спрашиваем заученные примеры. Если ребенок, в каком либо примере ошибся, повторите его три раза.

Делаем опять перерыв, минут десять на усваивание информации. Читать полностью »

математика, умножение

вычитание, деление, математика, начальная школа, сложение, умножение

Основные содержательные линии в математике – вычислительные навыки

13 Янв 2017 Рубрика: Математика

Отзывов (3) »

Продолжаем тему «основные содержательные линии курса математики начальной школы». В предыдущей статье мы рассмотрели такие линии, как «нумерации» и «величины». Продолжим далее по списку, представленному в предыдущей статье, и рассмотрим освоение учениками начальной школы вычислительных навыков.

Сложение и вычитание

В первом классе начальной школы дети осваивают сложение и вычитание в пределах 10, а также в пределах 100 без перехода через десяток.

Во втором классе сложение и вычитание осваивается уже сначала в пределах 20 с переходом через десяток, затем в пределах 100, также с переходом через десяток. Также осваивается письменное вычисление двухзначных чисел «в столбик».

В третьем классе осваивается сложение с переходом через разряд в пределах 10000, а также вычитание с переходом через разряд в пределах 1000. Дети устно складывают и вычитают круглые числа в пределах 1000, письменно – трехзначные числа.

В четвертом классе осваивается сложение и вычитание многозначных чисел, уже в пределах 1000000. Устно складывают и вычитают круглые числа, такие как тысячи и миллионы, а письменно – многозначные числа в пределах миллиона.

На нашем сайте Вы можете посмотреть видеоуроки сложение и вычитание.

Умножение и деление

Освоение таких вычислительных навыков, как умножение и деление начинается со второго класса, здесь осваивается таблица умножения, а также соответствующие случаи деления.

В третьем классе осваивается умножение трехзначных чисел на однозначное число, а также деление с остатком. Деление осуществляется трехзначных чисел на однозначное число, берутся простые случаи. Устно осуществляется внетабличное умножение двухзначных чисел на однозначные, умножение и деление на 10 и на 100, а также умножение и деление десятков на однозначное число. Письменно умножаются и делятся трехзначные числа на однозначные.

В четвертом классе осваивается умножение и деление многозначных чисел на двухзначные и трехзначные числа в пределах миллиона. Устно вычисляются круглые числа, а именно умножение и деление на двузначное число в пределах 100. Письменно умножаются и делятся многозначные числа на двузначные и трехзначные числа.

О том, что такое умножение и деление Вы можете прочитать на нашем сайте, а также здесь Вы можете найти информацию о том как выучить таблицу умножения.

На этом мы прервем наши исследования и продолжим их в следующей статье “найти значение выражения“.

Если вы хотите получать информацию о новых статьях и проектах нашего сайта, то подпишитесь на рассылку новостей сайта. Всего вам наилучшего и успехов. Спасибо.

Числовые равенства и неравенства

16 Янв 2015 Рубрика: Математика

деление, математика, основные правила, умножение

Числовые равенства

Чтобы получить запись, называемую числовым равенством, надо два числовых выражения соединить знаком равенства (=).

Пример:

Представленный пример является верным числовым равенством, но числовое равенство может быть неверным:

Давайте разберем свойства числовых равенств.

Если числовое равенство верно, то прибавив к обеим частям этого равенства одно и тоже число мы получим верное числовое равенство.

Например:

Проверим равенство

(12 + 3) = (9 + 6)

12 + 3 = 15 и 9 + 6 = 15

Равенство верно, теперь проверим свойство

(12 + 3) + (5 – 2) = (9 + 6) + (5 – 2)

15 + (5 – 2) = 15 + (5 – 2)

18 = 18

В обоих случаях равенства верны

То же самое произойдет, если мы вычтем одно и то же числовое выражение из обеих частей верного числового равенства.

Проверим это свойство на предыдущем примере заменив действие сложение на вычитание:

(12 + 3) – (5 – 2) = (9 + 6) – (5 – 2)

15 + (5 – 2) = 15 + (5 – 2)

12 = 12

Как мы видим равенство верно.

Если числовое равенство верно, то умножив обе части этого равенства на одно и тоже числовое выражение мы получим верное числовое равенство.

Проверим и это свойство:

(75 – 3) = (15 + 57)

75 – 3 = 72 и 15 + 57 = 72 это равенство верно

(75 – 3) · (10 – 2) = (15 + 57) · (10 – 2)

72 · (10 – 2) = 72 · 8 = 576

576 = 576

Свойство доказано.

Читать полностью »

Умножение в столбик

24 Март 2014 Рубрика: Математика

Умножение многозначных или многоразрядных чисел удобно производить письменно в столбик, последовательно умножая каждый разряд. Давайте разберем, как это делать. Начнем с умножения многоразрядного числа на одноразрядное число и постепенно увеличим разрядность второго множителя.

Для того чтобы умножить в столбик два числа, разместите их одно под другим, единицы под единицами, десятки под десятками и так далее. Сравните два множителя и меньший разместите под большим. Затем начинайте умножать каждый разряд второго множителя на все разряды первого множителя.

Умножение многозначного числа на однозначное

Пишем однозначное число под единицами многозначного.

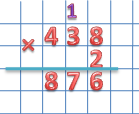Умножаем 2 последовательно на все разряды первого множителя:

Умножаем на единицы:

8 × 2 = 16

6 пишем под единицами, а 1 десяток запоминаем. Для того, чтобы не забыть пишем 1 над десятками.

Умножаем на десятки:

3 десятка × 2 = 6 десятков + 1 десяток(запоминали) = 7 десятков. Ответ пишем под десятками.

Умножаем на сотни:

4 сотни × 2 = 8 сотен. Ответ пишем под сотнями. В результате получаем:

438 × 2 = 876

Умножение многозначного числа на многозначное

Умножим трехзначное число на двухзначное:

924 × 35

Пишем двухзначное число под трехзначным, единицы под единицами, десятки под десятками.

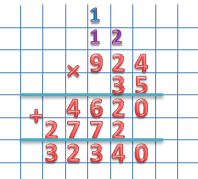1 этап: находим первое неполное произведение, умножив 924 на 5.

Умножаем 5 последовательно на все разряды первого множителя.

Умножаем на единицы:

4 × 5 = 20 0 пишем под единицами второго множителя, 2 десятка запоминаем.

Умножаем на десятки:

2 десятка × 5 = 10 десятков + 2 десятка (запоминали) = 12 десятков, пишем 2 под десятками второго множителя, 1 запоминаем.

Умножаем на сотни:

9 сотен × 5 = 45 сотен + 1 сотня (запоминали) = 46 сотен, пишем 6 под разрядом сотен, а 4 под разрядом тысяч второго множителя.

924 × 5 = 4620

2 этап: находим второе неполное произведение, умножив 924 на 3.

Умножаем 3 последовательно на все разряды первого множителя. Ответ пишем под ответом первого этапа, сдвинув его на один разряд влево.

Умножаем на единицы:

4 × 3 = 12 2 пишем под разрядом десятков, 1 запоминаем.

Умножаем на десятки:

2 десятка × 3 = 6 десятков + 1 десяток (запоминали) = 7 десятков, пишем 7 под разрядом сотен.

Умножаем на сотни:

9 сотен × 3 = 27 сотен, 7 пишем в разряд тысяч, а 2 в разряд десятков тысяч.

3 этап: складываем оба неполных произведения.

Складываем поразрядно, учитывая сдвиг.

В результате получаем:

924 × 35 = 32340 Читать полностью »

Учим таблицу умножения. День шестой

06 Окт 2012 Рубрика: Математика, Основные правила

Отзывов (3) »

Было трудно, но надо еще немного постараться и «золотой ключик у нас будет в кармане». Итак, мы продолжаем учить таблицу умножения и сегодня учим таблицы на 7, на 8 и на 9.

Тем, кто только что к нам присоединился, стоит сначала изучить предыдущие уроки. Все ссылки есть в статье “Как выучить таблицу умножения“.

Прежде чем начать, повторяем выученные, на прошлом занятии, примеры: (2 × 7), (3 × 7), (7 × 4), (5 × 7), (6 × 7) а также (2 × 8), (3 × 8), (8 × 4), (5 × 8) и (6 × 8). Если не возникло проблем, то продолжаем. Если что-то забыли, то повторите еще раз и сделайте перерыв.

I группа

Проговариваем примеры по три раза, ребенок повторяет за Вами и смотрит на пример.

Семью семь – сорок девять

Семью восемь – пятьдесят шесть

Семью девять – шестьдесят три

Спрашиваем всю таблицу на 7, начиная с:

7 × 8 = ?

7 × 7 = ?

7 × 9 = ?

2 × 7 = ?

7 × 4 = ?

3 × 7 = ?

5 × 7 = ?

6 × 7 = ?

Как только добились правильных ответов на все примеры, делаем перерыв 15 минут. После перерыва опять вспоминаем таблицу на 7. Делаем перерыв 15 минут. Читать полностью »

Учим таблицу умножения. День пятый

24 Сен 2012 Рубрика: Математика, Основные правила

Мы продолжаем помогать нашим детям учить таблицу умножения. Ссылки на предыдущие уроки смотрите в статье “Как выучить таблицу умножения”. На этом уроке мы будем учить сразу две таблицы, так как мы уже знаем половину этих таблиц. Но начнем урок с повторения предыдущего урока. Пусть Ваш ребенок вспомнит таблицу умножения на 4, а затем на 2 и на 3.

Если все вспомнили правильно, продолжаем урок.

Итак, часть таблицы, даже большую, мы уже знаем. Осталось совсем немного.

Сегодня будем учить таблицу умножения на 5 и на 6. Так как их мы уже на половину знаем: (5 × 2), (5 × 3) и (5 × 4), а также (6 × 2), (6 × 3) и (6 × 4). Перед началом занятий, повторите их с ребенком. Напомните ему, что если он не вспомнил сколько будет 5 × 3, пусть переставит множители местами. Мы учили 3 × 5 = 15. И так далее.

I группа

Проговариваем по три раза каждый пример, ребенок повторяет за Вами:

Пятью пять – двадцать пять

Пятью шесть – тридцать

Пятью семь – тридцать пять

Сразу спрашиваем

5 × 6 = ?

5 × 5 = ?

5 × 7 = ?

5 × 4 = ?

5 × 2 = ?

5 × 3 = ?

Если ребенок все отвечает правильно, делаем перерыв 15 минут. В противном случае, повторяем примеры, в которых ребенок ошибся.

II группа

Пятью восемь – сорок

Пятью девять – сорок пять

Шестью шесть – тридцать шесть

Сразу спрашиваем:

5 × 9 = ?

5 × 5 = ?

5 × 8 = ?

5 × 6 = ?

5 × 7 = ?

6 × 6 = ?

5 × 4 = ?

5 × 2 = ?

5 × 3 = ?

Добиваемся всех правильных ответов, делаем перерыв 15 минут. После перерыва еще раз повторяем заученные примеры, затем перерыв 15 минут. Читать полностью »