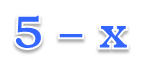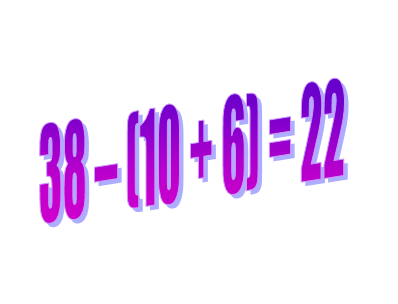В этой статье мы поговорим о компьютере. Она открывает рубрику «Информатика». Мы поговорим о том:
С самой древности люди умели считать. Все началось, скорее всего, со счета на пальцах. Но пальцев оказалось меньше, чем, то чего надо было сосчитать,да и запоминать большие числа было трудно, вот тогда, вероятно, и появилась первая письменность.
Как появился компьютер
Со временем люди стали изобретать счетные приборы. Сначала это были простые дощечки, на которых выкладывались камешки.
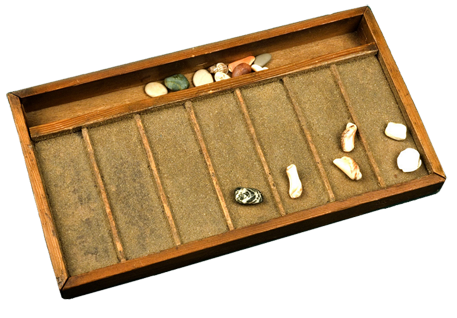Затем дощечки усовершенствовали, разделив на ячейки и насыпав песка в них, для того, чтобы камешки не ездили по дощечке.
Так появился первый счетный прибор, его называли «Абак». В переводе с греческого Абак значит «камешек». Он был распространен в основном в древней Греции и Риме, но затем о нем узнали другие страны.
Например, в Китае в 12 веке изобрели одну из разновидностей Абака, которую назвали Суаньпань. Этот прибор уже больше походил на счеты, а принцип счета на таком приборе, был основан на пятеричной системе счисления.
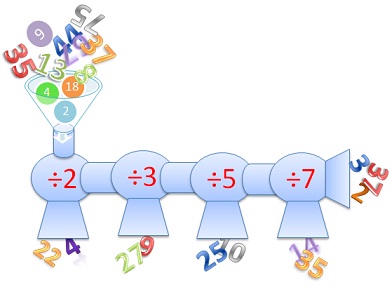
Мы привыкли к десятичной системе счисления, она связана с тем, что у человека 10 пальцев. В десятичной системе мы считаем десятками:
Первый десяток от 0 до 9:
0 1 2 3 4 5 6 7 8 9
Далее к цифрам первого десятка, слева добавляется единица:
10 11 12 13 14 15 16 17 18 19
Затем каждый десяток озаглавливается следующей цифрой по порядку:
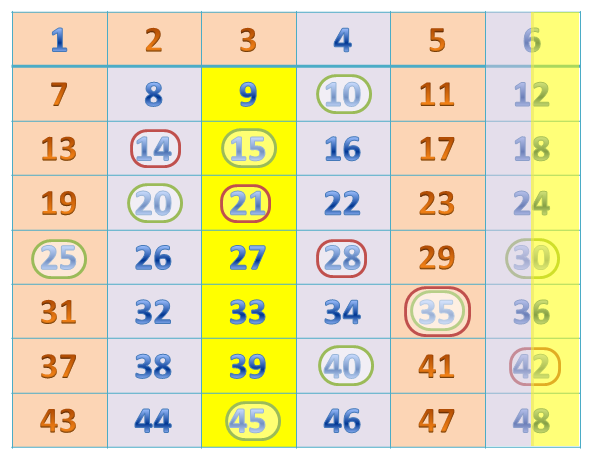
20 21 22 23 24 25 26 27 28 29
30 31 32 33 34 35 36 37 38 39
И так далее до 99, затем добавляют третью цифру слева – сотни, которые тоже чередуются по порядку, затем тысячи и так далее.
Но люди изобрели не только десятичную систему, но и двоичную, пятеричную, восьмеричную, шестнадцатеричную и другие системы счисления.
Об этом мы поговорим в других статьях этой рубрики. А сейчас вернемся к счетным приборам. Итак, прибор Суаньпань, в 16 веке усовершенствовали и назвали Соробан. Этот прибор до сих пор используется в школах Японии и считается самым быстрым механическим счетным устройством.
В России Абак преобразовался в счеты. Счеты были изобретены в 16 веке и использовались до конца 20 века, бухгалтерами и продавцами в магазинах.
Первая же счетная машина была изобретена в 17 веке французским ученым Блезом Паскалем. Современники ученого назвали этот прибор «паскалевым колесом». Он умел выполнять только сложение и вычитание.
Со временем он приобрел другое имя – арифмометр. Это был настоящий прорыв. Впервые машина делала то, что мог только человек.
Затем арифмометры усовершенствовались. Сначала они были механическими, потом стали использовать электромоторы.
Но первые электронно–вычислительные машины (ЭВМ) или компьютеры, появились ближе к середине прошлого века.
Но эти компьютеры были не такими, к каким мы привыкли. Эти машины занимали целые здания, а для управления и обслуживания таких машин требовалось много человек.
Со временем технологии производства ЭВМ совершенствовались. Размеры компьютеров становились все меньше и меньше, а вычислительные мощности всё больше. Так появились персональные компьютеры, помещавшиеся на рабочем столе.
Такой компьютер предназначен для работы одного человека (персоны). Персональные компьютеры люди покупают домой как для работы, так и для развлечения. С их помощью можно смотреть фильмы, просматривать картинки и фотографии, производить расчеты (например, бюджета семьи), или играть в компьютерные игры.
Компьютер теперь помогает человеку во всем, он управляет машинами, самолетами, поездами. Даже дома мы можем увидеть приборы, работой которых управляет компьютер, например стиральные и посудомоечные машины.
Компьютер теперь стал главным помощником человека, его применяют для обучения школьников и студентов. Он применяется в медицине для обследования и уточнения диагноза пациента. Без компьютера невозможно полететь в космос, ведь всеми приборами управляет он – компьютер. Читать полностью »
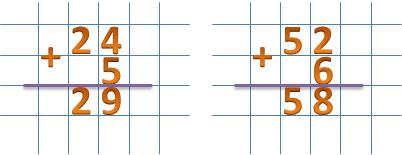
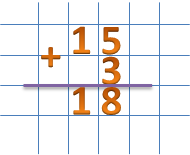Теперь сложим единицы первого и второго числа:
